Diffie-Hellman 密钥交换
Diffie-Hellman 密钥交换(Diffie-Hellman key exchange)是 1976 年由 Whitfield Diffie 和 Martin Heilman 共同发明的一种算法。使用这种算法,通信双方仅通过交换一些可以公开的信息就能够生成出共享的秘密数字,
而这一秘密数字就可以被用作对称密码的密钥。IPsec 中就使用了经过改良的 Diffie-Hellman 密钥交换。
虽然这种方法的名字叫 “密钥交换”,但实际上双方并没有真正交换密钥,而是通过计算生成出了一个相同的共享秘钥。因此,这种方法也称为 Diffie-Hellman 密钥协商(Diffie-Hellmankey agreement)。
Diffie-Hellman 密钥交换的步骤
现在我们假设帕蒂和鲍勃需要共享一个对称密码的密钥,然而双方之间的通信线路已经被窃听者窃听了。这时,帕蒂和鲍勃可以通过以下方法进行 Diffie-HeUman 密钥交换,从而生成共享密钥。
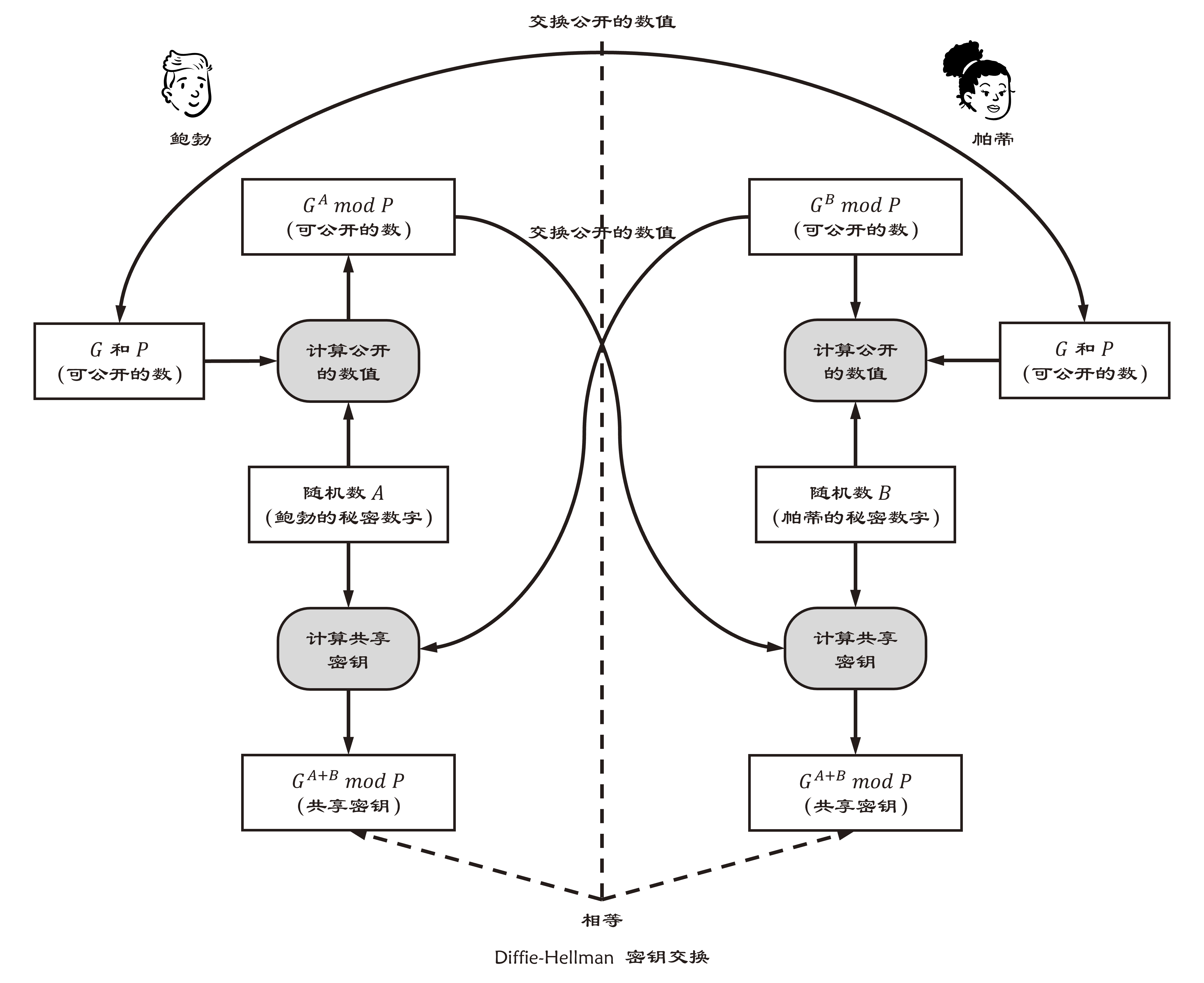
(1) 鲍勃向帕蒂发送两个质数 P 和 G
P 必须是一个非常大的质数,而 G 则是一个和 P 相关的数,称为生成元(generator)。G 可以是一个较小的数字。
P 和 G 不需要保密,被窃听者获取也没关系。此外,P 和 G 可以由鲍勃和帕蒂中的任意一方生成。
(2) 鲍勃生成一个随机数 A
A 是一个 l ~ P-2 之间的整数。这个数是一个只有鲍勃知道的秘密数字,没有必要告诉帕蒂, 也不能让窃听者知道。
(3) 帕蒂生成一个随机数 B
B 是一个 l ~ P-2 之间的整数。这个数是一个只有鲍勃知道的秘密数字,没有必要告诉鲍勃, 也不能让窃听者知道。
(4) 鲍勃将 GA mod P 这个数发送给帕蒂
这个数让窃听者知道也没关系。
(5) 帕蒂将 GB mod P 这个数发送给鲍勃
这个数让窃听者知道也没关系。
(6) 鲍勃用帕蒂发过来的数计算 A 次方并求 mod P
这个数就是共享密钥。
鲍勃计算的密钥 = (GB mod P)A mod P = GB x A mod P
(7) 帕蒂用鲍勃发过来的数计算 B 次方并求 mod P
帕蒂计算的密钥 = (GA mod P)B mod P = GA x B mod P
窃听者能计算出密钥吗
在步骤(1)~(7)中,双方交换的数字(即能够被窃听者知道的数字)一共有 4 个:P、G,GA mod P 和 GB mod P。根据这 4 个数字计算出鲍勃和帕蒂的共享密钥(GA x B mod P)是非常困难的。
椭圆曲线 Diffie-Hellman 密钥交换
Diffie-Hellman 密钥交换是利用“离散对数问题”的复杂度来实现密钥的安全交换的,如果将“离散对数问题”改为“椭圆曲线上的离散对数问题”,这样的算法就称为椭圆曲线 Diffie-Hellman 密钥交换。
椭圆曲线 Diffie-Hellman 密钥交换在总体流程上是不变的,只是所利用的数学问题不同而已。椭圆曲线 Diffie-Hellman 密钥交换能够用较短的密钥长度实现较高的安全性。
曲线类型
-
p192 (NIST P-192): 192位素数域椭圆曲线,由美国国家标准与技术研究院(NIST)推荐,安全性较低,不推荐用于新系统。
-
p224 (NIST P-224): 224位素数域椭圆曲线,NIST推荐,安全性比P-192高。
-
p256 (NIST P-256): 256位素数域椭圆曲线,NIST推荐,广泛应用于TLS等协议,提供良好的安全性和性能平衡。
-
p384 (NIST P-384): 384位素数域椭圆曲线,NIST推荐,提供更高安全性。
-
p521 (NIST P-521): 521位素数域椭圆曲线,NIST推荐的最高安全级别曲线,计算开销较大。
-
curve25519 (X25519): 设计用于高效的密钥交换,广泛应用于现代加密协议,提供良好的性能和安全性,在这里也可用于 ECIES。
-
secp256k1 (Bitcoin curve): 256位Koblitz曲线,比特币和其他加密货币使用,非NIST标准,但在区块链领域广泛应用。
密钥格式
-
PKCS#8: 更通用,支持多种算法(如RSA、DSA、EC等),结构更灵活,可以包含额外信息。
-
RAM: 原始的非对称密钥格式,通常是直接的密钥数据,没有额外的封装或格式化,可能更加紧凑,但缺乏额外的元数据信息,在一些特定的应用场景中使用,但不如标准格式普遍。
-
DEM: 不是一种密钥格式,而是一种加密机制,通常用于混合加密系统中,使用对称加密来加密实际数据,然后用非对称加密来保护对称密钥,结合了对称加密的效率和非对称加密的安全性。
使用随机填充
在 RSA 的实际使用中,通常会在加密前会向明文中添加一些随机数据,使得每次加密的输入都不同,从而产生不同的密文。目的是增加加密的安全性,防止各种潜在的攻击,如重放攻击、选择明文攻击等。虽然每次加密结果看起来不同,
但使用相同的私钥仍然可以正确解密。但在某些特定情境下我们又需要不做随机的填充,因此在勾选上“使用随机填充”后会在加密过程中添加随机数,反之亦然。
