XOR
XOR 的全称是 exclusive or,在中文里叫异或。尽管名字看起来很复杂,但这种运算本身一点也不难。
1 个比特的 XOR
0 XOR 0 = 0 (0 与 0 的 XOR 的结果为 0)
0 XOR 1 = 1 (0 与 1 的 XOR 的结果为 1)
1 XOR 0 = 1 (1 与 0 的 XOR 的结果为 1)
0 XOR 0 = 0 (0 与 0 的 XOR 的结果为 0)
如果将 0 理解为偶数,将 1 理解为奇数,就可以将 XOR 和一般的加法运算等同起来。
偶数(0) + 偶数(0) = 偶数(0)
偶数(0) + 奇数(1) = 奇数(1)
奇数(1) + 偶数(0) = 奇数(1)
奇数(1) + 奇数(1) = 偶数(0)
由于 XOR 和加法运算很相似,因此一般用 + 和 ◯ 组合而成的的符号 ⊕ 来表示 XOR。
0 ⊕ 0 = 0 (0 与 0 的 XOR 的结果为 0)
0 ⊕ 1 = 1 (0 与 1 的 XOR 的结果为 1)
1 ⊕ 0 = 1 (1 与 0 的 XOR 的结果为 1)
0 ⊕ 0 = 0 (0 与 0 的 XOR 的结果为 0)
为了更加直观地理解 XOR,大家可以想象一下黑白棋中的棋子。
我们将一个棋子保持原状(不翻)看作 0,将一个棋子翻转到另一面看作 1,那么 XOR 运算就相当于将黑白棋的一个棋子进行翻转的操作。
不翻(0) ⊕ 不翻(0) = 不翻(0) ———— 没有翻转过
不翻(0) ⊕ 翻转(1) = 翻转(1) ———— 翻转了一次
不翻(0) ⊕ 翻转(1) = 翻转(1) ———— 翻转了一次
翻转(1) ⊕ 翻转(1) = 不翻(0) ———— 翻转了两次,就等于没有翻转
通过上述场景,大家应该能够理解这样一个规律,即
两个相同的数进行 XOR 运算的结果一定为 0。
比特序列的 XOR
上面我们介绍了 1 个比特之间的 XOR运算,而如果是长比特序列之间的 XOR 运算,则只要对其中每个相应的比特进行 XOR 运算就可以了。假设我们将 0 1 0 0 1 0 0 这个比特序列称为 A,
将 1 0 1 0 1 0 1 0 这个比特序列称为 B,那么 A 与 B的 XOR 运算就可以像下面这样逐一对各个比特进行计算。和加法运算不同的是,XOR 中不需要进位。

由于两个相同的数进行 XOR 运算的结果一定为 0,因此如果将A ⊕ B 的结果再与 B 进行 XOR 运算,则结果会变回 A。也就是说,两个公式中的 B 会相互抵消。

可能大家已经发现了,上面的计算和加密、解密的步骤非常相似。
-
将明文 A 用密钥 B 进行加密,得到密文 A ⊕ B
-
将密文 A ⊕ B 用密钥 B 进行解密,得到明文 A
实际上,只要选择一个合适得 B,仅仅使用 XOR 就可以实现一个高强度的密码。
对同一个比特序列进行两次 XOR 就会回到最初的状态。我们不妨来看一幅由很多个点组成的图像。如果将白色的点作为 0,黑色的点作为 1,那么一幅黑白图像就可以表示为 0 和 1 的比特序列。
我们准备两幅图像,一幅画的是英文字母 D,另一幅是用 0 和 1 交替排列形成的图像(蒙版),这两张图像用 XOR 合并之后的样子如图 3-1 所示。从图中可以看出,执行一次蒙版操作后,原来
的图像被隐藏(掩盖)了,而执行两次蒙版操作后,就又可以得到原来的图像了。
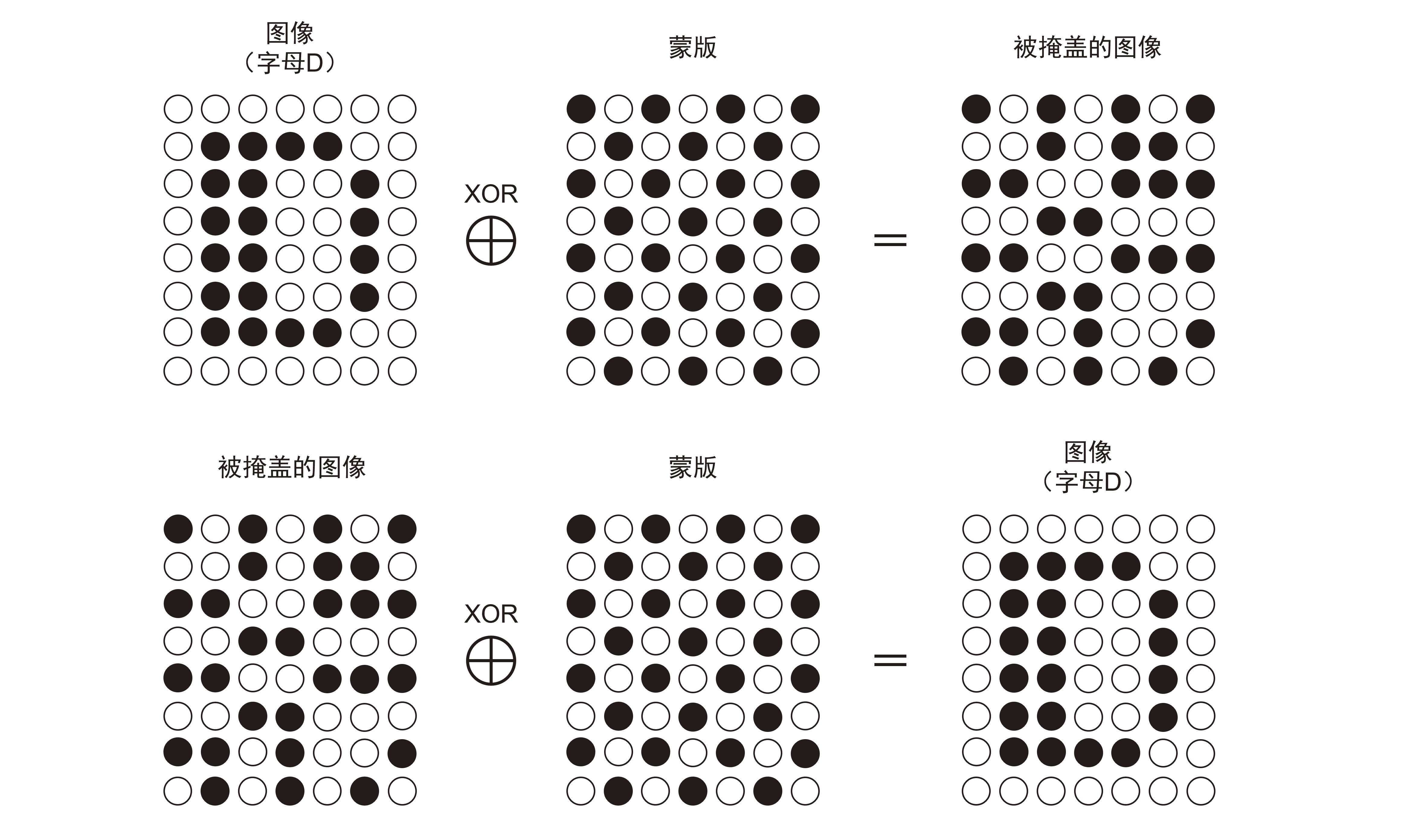
如果所使用的蒙版是完全随机的比特序列,则使用 XOR 就可以将原来的图像掩盖起来。但如果蒙版中的比特序列的排列是可以被推测出来的,那么实质上图像就没有被真正掩盖。对于密码技术来说,
“是否可以预测”是非常重要的一点。能够产生不可预测的比特序列,对于密码技术的贡献是巨大的。这种不可预测的比特序列就称为
随机数。


